Kruskal Algorithm in C: The Kruskal algorithm finds the minimum spanning tree where all the vertex is included and has minimum sum weight among the other vertex if considered. This algorithm has a logarithmic time complexity i,e (O (N log N)).
Minimum Spanning trees are subsets of spanning trees where the sum between the edges is minimal. With the help of the Kruskal algorithm, we will be able to find this graph.
What is the Kruskal Algorithm?
The Kruskal algorithm is used to find the minimum spanning tree that has all the vertex and minimum sum weight among the two vertices taken into consideration. The Kruskal algorithm consists of the same number of vertices as the input graph, with edges equal to vertex-1.

In the Kruskal algorithm, we start with edges in increasing order of their weights. We will add vertices to the resultant graph only if it does not form a cycle. We can use a greedy algorithm to solve the Kruskal algorithm as it finds the local optimal choice, which can be implemented using the greedy method.
What is a Spanning Tree?
A spanning tree is an acyclic graph that contains all the vertices and some edges. However, no two edges must form a cycle in the resultant spanning tree. There can be multiple spanning trees for a set of vertices. Hence, it is not unique.
There are two types of edges in a spanning tree. The ones that are in the output tree are called branch edges. The edges that are not included in the spanning tree are called cycle edges.
Learn Data Structure With PW Skills
Join our C++ with DSA course to learn the programming language C++ along with its important data structure. The course will sharpen your data structure and algorithmic skills. This course is covered completely by industry-level experts. Along with the course, you will receive many benefits such as exercises, PW Lab access, 1:1 doubt support, placement assistance, etc. Hurry and join our course to build a career in software development and relevant fields.
Minimum Spanning Tree Using Kruskal Algorithm
The steps below will help you learn how to use the Kruskal algorithm to create a minimum-spanning tree.
- Step 1: The first step is to arrange all the edges in an increasing order according to their weights.
- Step 2: Now, after arranging all the edges in increasing order, select the edge with the minimum weight value.
- Step 3: While adding the edges, you must check whether the edge forms a loop. If adding the edge creates a cycle, then do not add it to the spanning tree.
- Step 4: If the edge does not form a loop, then add it to the minimum spanning tree.
- Step 5: Repeat the step until all the edges equal to N-1 are added to the minimum spanning tree.
Example To Understand Kruskal Algorithm in Detail
Given below is a graph G(V, E) consisting of V as the vertices and E edges. This graph has 6 vertices and 8 edges. Now, we will use the Kruskal algorithm to find the minimum spanning tree using the graph given below.
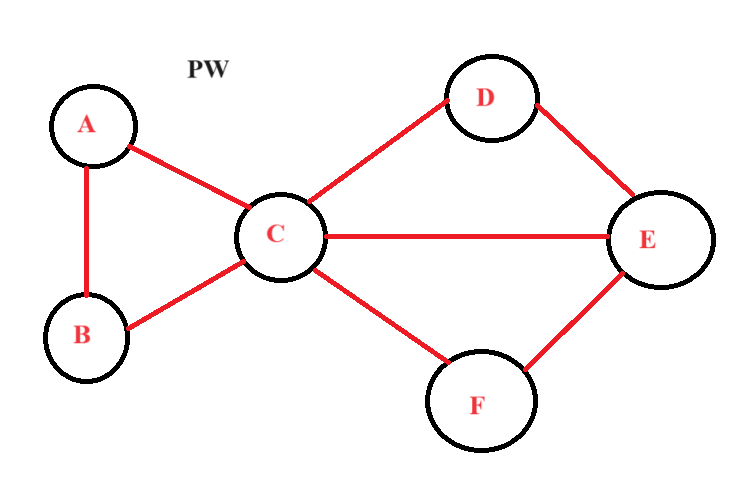
Now, the graph has vertices and edges arranged. We need to find the minimum spanning tree. Let us use the Kruskal algorithm to solve the graph.
Step 1: Check for any parallel or self-edges. If there are parallel edges, remove them from the output graph.
Step 2: Now arrange all the edges in a sorted list by their edge weights. For this, let us create a table to include the source vertex and destination vertex in a sorted order according to their weight.
|
Kruskal Algorithm in C |
||
|
Source vertex |
Destination Vertex |
Weight of the edge |
| B | C | 2 |
| C | F | 2 |
| C | D | 3 |
| D | E | 3 |
| F | E | 3 |
| A | B | 4 |
| A | C | 4 |
| A | E | 4 |
Now, start including the edges from the start in the sorted order as given in the table. Make sure that the edge included does not form a cycle in the graph.
Step 3: First, we will include the edges BC and CF with the minimum weight edges in the graph. Make sure that they do not form a cycle.
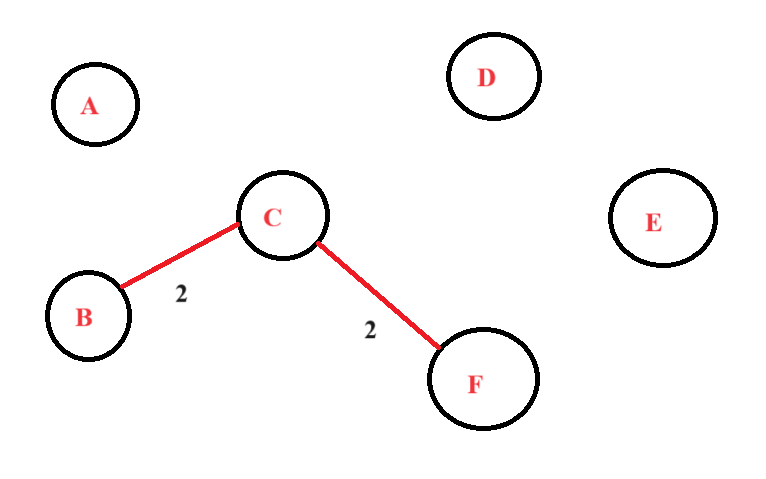
Step 4: Now, we will move to the next edge, i,e. CD, DE, and FE. But we will add only those edges that do not form a cycle in the graph. We conclude that DE and FE do not form a cycle when included in the graph. We will add them.
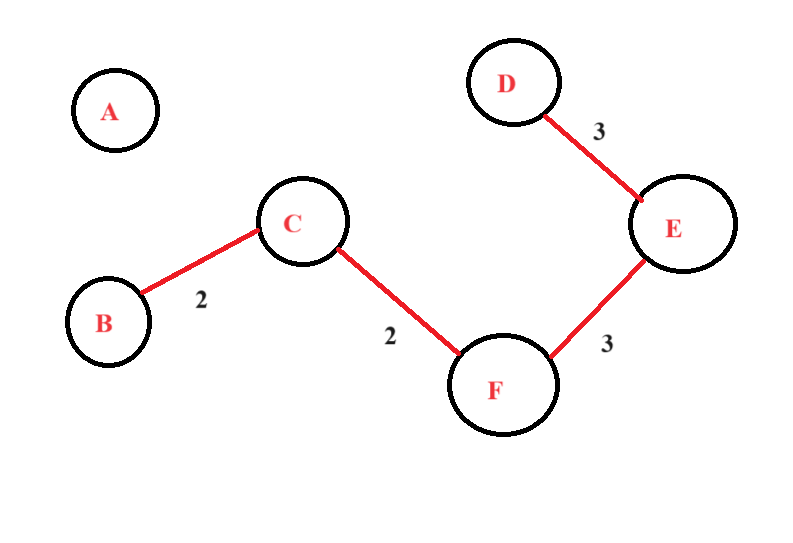
Step 5: Now, we will move ahead and look for the next set of possible edges for the graph. As we can see, only AB can be included without making a cycle. We will finally add AB to our final spanning tree.
This is the final spanning tree.
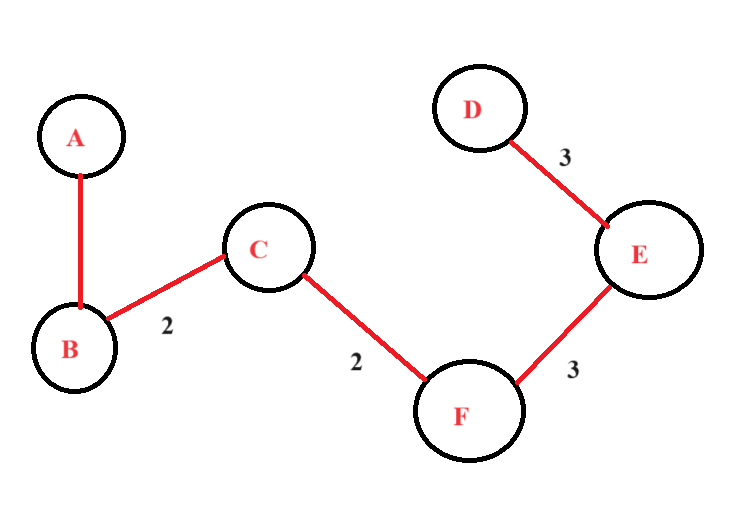
Step 6: Now, we will calculate the total cost of making this spanning tree using the Kruskal algorithm. For this, we will add all the edges included in the final spanning tree.
Cost = 4 + 2 + 2 + 3 + 3 = 14.
Also Read: Top 10 Mind Blowing Algorithmic Puzzles Which Every Developers must Try once
Important Facts About Kruskal Algorithm
Let us know some of the important highlights of the Kruskal algorithm here.
- The Kruskal algorithm finds the minimum spanning tree having all the vertices and one or more edge less.
- The number of vertices or nodes in the resulting minimum spanning tree is always the same as the last one.
- The number of edges is, however, reduced to N-1, where N is the number of vertices in the spanning tree.
- Make sure that the resultant spanning tree does not have any cycles.
Difference between Kruskal Algorithm and Prim’s Algorithm
The Kruskal algorithm and prim’s algorithm share many similarities as they are both used to find the minimum spanning tree. However, let us know some major differences between them.
|
Difference between Kruskal Algorithm and Prim’s algorithm |
|
| Kruskal Algorithm | Prim’s algorithm |
| It begins building the minimum spanning tree from the vertex having minimum weight in the graph. | It begins by making the minimum spanning tree from any one vertex given in the graph. |
| It is effective for sparse graphs. | It is optimal for dense graphs. |
| It works on disconnected components and also generates minimum spanning trees in a disconnected manner. | It works on connected components and generates minimum spanning trees in a connected manner. |
| It generates a minimum spanning tree from the least weighted graph. | It generates a minimum spanning tree from the root vertex of the graph. |
| It prefers heap data structures. | It prefers a list data structure. |
Implementation of Kruskal Algorithm in C
Here, we will go around checking the implementation of the Kruskal algorithm in C language. Check the table below.
|
Implementation of Kruskal Algorithm in C |
| #include <stdio.h>
#include <stdlib.h> // Structure to represent an edge in the graph struct Edge { int src, dest, weight; }; // Structure to represent a subset for union-find struct Subset { int parent; int rank; }; // Function prototypes int find(struct Subset subsets[], int i); void Union(struct Subset subsets[], int x, int y); void KruskalMST(struct Edge edges[], int V, int E); // Compare function for sorting edges based on weight int compare(const void* a, const void* b) { return ((struct Edge*)a)->weight – ((struct Edge*)b)->weight; } int main() { // Example graph represented by its edges int V = 4; // Number of vertices int E = 5; // Number of edges struct Edge edges[] = { {0, 1, 10}, {0, 2, 6}, {0, 3, 5}, {1, 3, 15}, {2, 3, 4} }; KruskalMST(edges, V, E); return 0; } // Find set of an element i (uses path compression technique) int find(struct Subset subsets[], int i) { if (subsets[i].parent != i) subsets[i].parent = find(subsets, subsets[i].parent); return subsets[i].parent; } // Perform union of two subsets (uses union by rank) void Union(struct Subset subsets[], int x, int y) { int xroot = find(subsets, x); int yroot = find(subsets, y); if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; else { subsets[yroot].parent = xroot; subsets[xroot].rank++; } } // Kruskal’s algorithm to find Minimum Spanning Tree (MST) void KruskalMST(struct Edge edges[], int V, int E) { // Allocate memory for subsets and initialize them struct Subset* subsets = (struct Subset*)malloc(V * sizeof(struct Subset)); for (int i = 0; i < V; i++) { subsets[i].parent = i; subsets[i].rank = 0; } // Sort edges in non-decreasing order by weight qsort(edges, E, sizeof(edges[0]), compare); // Initialize result as an empty array to store the MST struct Edge result[V]; int e = 0; // Index variable for result[] // Iterate through all sorted edges for (int i = 0; e < V – 1 && i < E; i++) { struct Edge next_edge = edges[i]; // Find sets of the source and destination vertices int x = find(subsets, next_edge.src); int y = find(subsets, next_edge.dest); // If including this edge does not cause a cycle, add it to the result if (x != y) { result[e++] = next_edge; Union(subsets, x, y); } } // Print the edges of the MST printf(“Edges in the Minimum Spanning Tree:\n”); for (int i = 0; i < e; i++) printf(“%d — %d Weight: %d\n”, result[i].src, result[i].dest, result[i].weight); // Free allocated memory free(subsets); } |
Implementation of Kruskal Algorithm With Python
Let us implement the Kruskal algorithm using Python programming language in the table below.
|
Implementation of Kruskal Algorithm using Python |
| class Graph:
def __init__(self, vertices): self.vertices = vertices self.edges = [] self.adjacency_list = {v: [] for v in vertices} def add_edge(self, u, v, weight): self.edges.append((u, v, weight)) self.adjacency_list[u].append((v, weight)) self.adjacency_list[v].append((u, weight)) def find_parent(self, parent, i): if parent[i] == i: return i return self.find_parent(parent, parent[i]) def union(self, parent, rank, x, y): root_x = self.find_parent(parent, x) root_y = self.find_parent(parent, y) if rank[root_x] < rank[root_y]: parent[root_x] = root_y elif rank[root_x] > rank[root_y]: parent[root_y] = root_x else: parent[root_y] = root_x rank[root_x] += 1 def kruskal(self): minimum_spanning_tree = set() parent = {} rank = {} for v in self.vertices: parent[v] = v rank[v] = 0 sorted_edges = sorted(self.edges, key=lambda x: x[2]) for edge in sorted_edges: u, v, weight = edge root_u = self.find_parent(parent, u) root_v = self.find_parent(parent, v) if root_u != root_v: minimum_spanning_tree.add(edge) self.union(parent, rank, root_u, root_v) return minimum_spanning_tree |
Implementation of Kruskal Algorithm With Java
Here we are using Java for implementing the Kruskal Algorithm. Check in the table here.
|
Implementation of Kruskal Algorithm using Java |
| // Import the required package
import Java.util.*; // Use the Kruskal algorithm to implement the minimum spanning tree. class KruskalAlgorithm { //create class Edge to create an edge of the graph that implements Comparable interface class Edge implements Comparable<Edge> { int source, destination, weight; public int compareTo(Edge edgeToCompare) { return this.weight – edgeToCompare.weight; } }; // creating subclass Union class Subset { int parent, value; }; //initialize vertices, edges and edgeArray int vertices, edges; Edge edgeArray[]; // using constructor to create a graph KruskalAlgorithm(int vertices, int edges) { this.vertices = vertices; this.edges = edges; edgeArray = new Edge[this.edges]; for (int i = 0; i < edges; ++i) edgeArray[i] = new Edge(); //create edge for all the edges given by the user } // applyKruskal() function to implement the kruskal algorithm for finding the minimum spanning tree. void applyKruskal() { // initialize finalResult array to store the final MST Edge finalResult[] = new Edge[vertices]; int newEdge = 0; int index = 0; for (index = 0; index < vertices; ++index) finalResult[index] = new Edge(); // using sort() method for sorting the edges for the kruskal algorithm Arrays.sort(edgeArray); // create an array of the vertices of type Subset for the subsets of vertices Subset subsetArray[] = new Subset[vertices]; // aloocate memory to create vertices subsets for (index = 0; index < vertices; ++index) subsetArray[index] = new Subset(); for (int vertex = 0; vertex < vertices; ++vertex) { subsetArray[vertex].parent = vertex; subsetArray[vertex].value = 0; } index = 0; // use for loop to pick the smallers edge from the edges and increment the index for next iteration while (newEdge < vertices – 1) { // create an instance of Edge for next edge Edge nextEdge = new Edge(); nextEdge = edgeArray[index++]; int nextSource = findSetOfElement(subsetArray, nextEdge.source); int nextDestination = findSetOfElement(subsetArray, nextEdge.destination); // Add only when the edge do not create a cycle in the minimum spanning tree. if (nextSource != nextDestination) { finalResult[newEdge++] = nextEdge; performUnion(subsetArray, nextSource, nextDestination); } } for (index = 0; index < newEdge; ++index) System.out.println(finalResult[index].source + ” – ” + finalResult[index].destination + “: ” + finalResult[index].weight); } // create findSetOfElement() method to get set of an element int findSetOfElement(Subset subsetArray[], int i) { if (subsetArray[i].parent != i) subsetArray[i].parent = findSetOfElement(subsetArray, subsetArray[i].parent); return subsetArray[i].parent; } // create performUnion() method to perform union of two sets void performUnion(Subset subsetArray[], int sourceRoot, int destinationRoot) { int nextSourceRoot = findSetOfElement(subsetArray, sourceRoot); int nextDestinationRoot = findSetOfElement(subsetArray, destinationRoot); if (subsetArray[nextSourceRoot].value < subsetArray[nextDestinationRoot].value) subsetArray[nextSourceRoot].parent = nextDestinationRoot; else if (subsetArray[nextSourceRoot].value > subsetArray[nextDestinationRoot].value) subsetArray[nextDestinationRoot].parent = nextSourceRoot; else { subsetArray[nextDestinationRoot].parent = nextSourceRoot; subsetArray[nextSourceRoot].value++; } } public static void main(String[] args) { int v, e; // get input using the scanner class from the users. Scanner sc = new Scanner(System.in); //show custom message System.out.println(“Enter number of vertices: “); //store user entered value into variable v v = sc.nextInt(); //show custom message System.out.println(“Enter number of edges”); //store user entered value into variable e e = sc.nextInt(); KruskalAlgorithm graph = new KruskalAlgorithm(v, e); for(int i = 0; i < e; i++){ System.out.println(“Enter source value for edge[“+ i +”]”); graph.edgeArray[i].source = sc.nextInt(); System.out.println(“Enter destination value for edge[“+ i +”]”); graph.edgeArray[i].destination = sc.nextInt(); System.out.println(“Enter weight for edge[“+i+”]”); graph.edgeArray[i].weight = sc.nextInt(); } // call applyKruskal() method to get MST graph.applyKruskal(); } } |
Complexity analysis of Kruskal Algorithm
The Kruskal algorithm is an optimal approach for solving the minimum spanning tree problems. Let us analyse the space and time complexity of the Kruskal algorithm below.
Kruskal algorithm uses sorting, union and find operations to implement the minimum spanning tree.
|
Time Complexity of Kruskal Algorithm |
| Best time complexity: O( E + log E ElogV)
Average time complexity: O( E log V) Worst time complexity: O( E log E) |
The space complexity of the Kruskal algorithm is determined by the data structure used for sorting and union operations. It is different based on the programming languages used. However, the space complexity of the Kruskal algorithm is approximately O (V).
For Latest Tech Related Information, Join Our Official Free Telegram Group : PW Skills Telegram Group
Kruskal Algorithm FAQs
What is the use of the Kruskal algorithm?
Ans: The Kruskal algorithm is used to find the minimum spanning tree that has all the vertex and minimum sum weight among the two vertices taken into consideration. The Kruskal algorithm consists of the same number of vertices as the input graph, with edges equal to vertex-1.
What is the average time complexity of the Kruskal Algorithm?
Ans: The average time complexity of the Kruskal Algorithm is O (E logV), where E is for edges and V is for vertices.
What is a spanning tree?
Ans: A spanning tree is an acyclic graph that contains all the vertices and some edges. However, no two edges must form a cycle in the resultant spanning tree. The minimum spanning tree is made using the minimum edges containing no cycle.
Is the Kruskal algorithm discontinuous?
Ans: The Kruskal algorithm works by breaking all the edges in a discontinuous manner and joining only the ones that follow the rules. The rules are minimum weight edges are given priority and no cycle should be present.






