Recursion in Python is a powerful tool that simplifies complex problems like tree traversal, searching algorithms, and mathematical computations. However, while it brings elegance to code, it also demands careful handling to avoid pitfalls like stack overflow and inefficiency.
In this blog, we will go through the magic of recursion, explore its real-world applications, and understand when to embrace it and when to opt for iteration.
What exactly is Recursion in Python?
Recursion means a function calling itself to solve a problem. It is a technique in which problems are broken down into smaller, similar subproblems, used primarily in problems like factorial computation, Fibonacci sequence, and tree traversal.
Basic Structure of Recursion in Python?
Recursion is a basic technique where a function calls itself to break a problem into smaller subproblems until it reaches the base case. The recursion function consists of two major parts, including the base case and the recursive case. Let us understand them in detail:
Base Case (Stopping Condition)
The base case is the condition that is used to stop the recursion. This is a stopping condition that prevents infinite recursion. The recursion in Python would continue indefinitely without a base case, causing a stack overflow error. The base case typically handles the simplest instance of the problem.
Let us see an example of the base case in the factorial calculation:
Example of Base Case in Factorial Calculation |
|---|
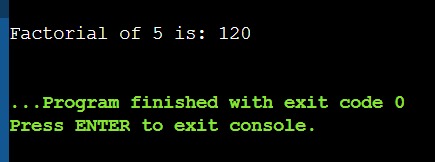
| def factorial(n):
if n == 0 or n ==1: return 1 else: return n * factorial (n – 1) n=5 ans = factorial(n) print(“Factorial of”,n,”is:”, ans) |
| Here, “If n == 0” is the base case that stops the recursion in Python
|
Recursive Case (Self-Calling Condition)
The recursive case is the part where the function calls itself to break the problem into smaller instances. It is where the function calls itself with a smaller or simpler version of the problem. It should always work toward the base case to prevent infinite recursion.
Let us see an example of the recursive case in the factorial calculation:
Example of Recursive Case in Factorial Calculation |
|---|
| def factorial(n):
if n == 0 or n ==1: return 1 else: return n * factorial (n – 1) n=5 ans = factorial(n) print(“Factorial of”,n,”is:”, ans) |
| Here, factorial (n – 1) is the recursive case that reduces the problem size step-by-step
|
General Structure of a Recursive Function
A general structure of a recursive function that can be used as a template for recursive functions in Python.
General Structure of a Recursive Function |
|---|
| def recursive_function(parameters):
if base_condition: return result else: return recursive_function(smaller_problem) |
Recursion vs. Iteration
Recursion is like taking one step and telling yourself, “I’ll figure out the rest the same way!” whereas iteration is when you repeatedly lift one foot after another until you reach the top. Both approaches get the job done, but they have distinct styles.
Recursion is a function that calls itself repeatedly to break a problem into smaller subproblems until a base condition is met, whereas iteration uses loops to execute a block of code repeatedly until a stopping condition is met.
Example of Printing Numbers from 5 to 1 Using Recursion and Iteration
Check a simple example of printing numbers from a range of value using simple recursion in Python language.
Countdown using Recursion in Python |
|---|
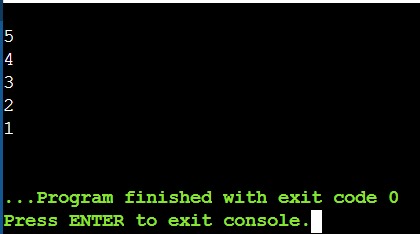
| def countdown(n):
if n <= 0: return print (n) countdown(n – 1) countdown(5) |
 |
Similarly, we can solve the same problem using iteration, let us see how:
Countdown Using Iteration in Python |
|---|
| def countdown(n):
while n > 0: print (n) n -= 1 countdown(5) |
 |
A Quick Tabular Difference Between Recursion and Iteration
Check some quick differences between Recursion and Iteration in programming language in the table below.
Recursion vs. Iteration |
||
|---|---|---|
| Feature | Recursion | Iteration |
| Definition | A function calls itself to solve smaller instances of the problem. | A loop executes a block of code repeatedly until a condition is met. |
| Structure | Uses function calls and a base case to stop recursion. | Uses for or while loops with a condition to stop execution. |
| Flow Control | Function calls are pushed onto the call stack until the base case is reached. | A loop updates variables directly and executes repeatedly. |
| Termination | Stops when the base case is met. | Stops when the loop condition becomes false. |
| Memory Usage | It consumes more memory due to the function call stack. | Uses constant memory (O(1)) as it doesn’t store previous states. |
| Performance | Can be slower due to function call overhead. | Faster because it avoids function calls. |
| Complexity | Time Complexity: Usually O(n), but can be optimized (e.g., memorization). Space Complexity: O(n) due to recursive calls. | Time Complexity: Usually O(n). Space Complexity: O(1) as no extra stack memory is used. |
| Risk | This can lead to a stack overflow if the recursion depth is too high. | No stack overflow risk as execution remains within a single function. |
| Use Cases | Best suited for problems with recursive structures (e.g., tree traversal, divide and conquer algorithms, backtracking). | Best for problems requiring simple repetition (e.g., iterating over arrays, loops). |
| Code Readability | Often more elegant and concise for complex problems like DFS, Fibonacci, and tree traversal. | More straightforward and easier to debug for simple loops. |
Advantages of Recursion
Recursion in Python is best for problems that have a recursive structure, such as trees, graphs, divide-and-conquer, and many more. Some of the major benefits of recursion are:
- Simplicity and Code Readability: Recursive solutions often require fewer lines of code compared to iterative solutions. They closely match the natural structure of many problems, making them easier to understand.
- Solving Problems with Recursive Structure: Some problems are naturally recursive, meaning they are easier to solve using recursion than iteration.
- Useful for Backtracking: Recursion is ideal for problems involving exploration and decision trees, such as sudoku solver, N-Queens Problems, Maze Solving, and many more.
- Eliminates Need for Explicit Stack Management: Recursion naturally uses the call stack to track function calls, removing the need for manually maintaining a stack. This is especially useful in DFS-based problems.
Read More: Top Coding Competition Platforms In 2025 For Everyone
Disadvantages of Recursion
Recursion in Python is elegant but can lead to a stack overflow if not carefully handled. Iteration is better for efficiency and avoids function call overhead. Memoization can optimize recursive functions and avoid redundant calculations. Some of the major disadvantages of recursion are:
- Consumes More Memory: Every recursive call is stored in the call stack, leading to high memory consumption. If the recursion depth is too high, it causes a stack overflow error.
- Slower due to Function Call Overhead: Every recursive call adds overhead, as Python needs to push function context onto the stack, execute function logic, and pop function context after execution. This makes recursion slower than iteration in many cases.
- Harder to Debug: Tracing recursive calls is difficult because the function keeps calling itself, making it harder to track values. Debugging tools show multiple function calls, which can be confusing.
- Iteration is Often Simpler and More Efficient: Many problems that can be solved using recursion can also be solved with loops which are easier to understand, and are more efficient in terms of memory and execution speed.
Learn DSA With Python with PW Skills
Become a skilled programmer in Python with Decode DSA with Python on PW Skills. Get in-depth knowledge of the programming language Python with practice exercises, module assignments, and real world projects. Get a completely self paced course with pre-recorded tutorials on the platform.
Recursion in Python FAQs
Q1. What is Recursion?
Ans. Recursion means a function calling itself to solve a problem. It is a technique in which problems are broken down into smaller, similar subproblems, used primarily in problems like factorial computation, Fibonacci sequence, and tree traversal.
Q2. What is a Base case in a recursion function in Python?
Ans. The base case is the condition that is used to stop the recursion. This is a stopping condition that prevents infinite recursion.
Q3. What is the difference between Recursion and Iteration?
Ans. Recursion is a function that calls itself repeatedly to break a problem into smaller subproblems until a base condition is met, whereas iteration uses loops to execute a block of code repeatedly until a stopping condition is met.