Coin flipping, die rolling, and some quick glances at your weather app to find out tomorrow’s forecast are all trivial moments in our lives. Each one of them is fueled by Probability Theory.
Imagine, then, that you discriminate your doctor’s medicine prescription by the probabilities of success, that you will put together an investment portfolio using a probability model, or that your favorite sports team will measure its winning odds before a crucial match. Probability Theory silently builds predictions, risk assessments, and decisions in the uncertain world.
What is it? How would you use it (students studying for exams, professionals analyzing data, or just curious people wondering how casinos make money never actually lose) all could really benefit from learning it? Let’s dive in.
What is Probability Theory?
Definition of Probability Theory:
Probability Theory is like the arm of mathematics that concerns itself with uncertainty studying how one event’s opportunity can be measured against another, all to at least mention that thing called likelihood.
Simply put: What are the chances?
- How likely is it to rain tomorrow?
- What are the odds that I’ll get a red card from the pack?
- What are the odds that your friend will be on time? (Mathematically low, perhaps!)
A number between 0 and 1 describes likelihood in Probability Theory.
- 0 means impossible.
- 1 means certain.
- In between indicates intermediate levels of probability.
![]() Join Our Data Science Telegram Channel
Join Our Data Science Telegram Channel
![]() Join Our Data Science WhatsApp Channel
Join Our Data Science WhatsApp Channel
Probabilistic Basics: Foundations
Before we start delving into formulas, let’s do the grounding blocks of Probability Theory with the basics.
Experiment- Any action that produces an outcome.
Example: Rolling a dice.
Outcome- Result of the experiment.
Example: Rolling a 4.
Sample Space (S) – The set of all possible outcomes.
Example: For a dice → {1, 2, 3, 4, 5, 6}.
Event (E) – Subset of sample space; something specific we are interested in.
Example: Rolling an even number → {2, 4, 6}.
Probability of Event (P(E)) – Calculated like:
![]()
Example: Probability of rolling a 4 = 1/6.
Probability Theory Formulas Everyone Should Know
Applying the practical toolkit: the most important Probability Theory formulas.
- The Classical Probability Formula
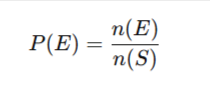
Where:
n (E) = number of favorable outcomes
n (S) = total possible outcomes
- Complementary Probability
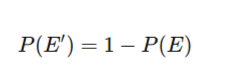
Example: If it rains 30% of the time, it doesn’t rain 70% of the time.
- The Addition Rule of Probability
For mutually exclusive events A and B:
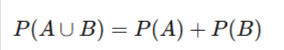
For non-mutually exclusive events:
![]()
- The Multiplication Rule of Probability
For independent events:
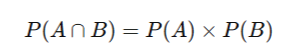
Example: Probability of rolling a 6 and flipping heads = (1/6) × (1/2) = 1/12.
- Conditional Probability
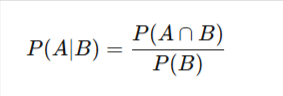
This tells us the probability of A happening given B has already happened.
- Bayes Theorem
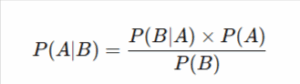
This is what I consider the diamond of modern statistics. It caches the probability of some event as new evidence comes in. Doctors and machine learning engineers use it, as do detectives in real-life situations.
Probability Theory Example- Make it Simple
This grounding in a real-life example.
Scenario:
You’re playing cards, what are the chances of drawing an Ace?
Total cards in a deck = 52
Total Aces = 4
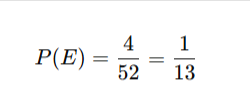
So, probability = 7.7%.
But what if you ask: What is the probability of drawing an Ace OR a King?
Aces = 4
Kings = 4
Favorable Outcomes = 8
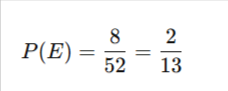
Now you see how formulas adapt to questions.
Why Learn Probability Theory?
If math seems far away, this is pretty much the reality check: In probability, the world runs.
- Googles search engine predicts what you want to say just before you finish typing-probability.
- Netflix knows exactly which series you should consider for your next bingeing-probability.
- Your doctor prescribes a medicine that has an 85 percent chance of success-probability.
- Insurance companies define your premium-your risk analysis-probability.
Understanding probability makes you a better examiner as well as him sharper in aspects of choosing life.
Applications of Probability Theory in Real Life
Probability Theory is not just about studying mathematics; in fact, it gets very real when applied to everyday lives and the world.
- Weather Forecasting-Meteorologists give the likelihood of an occurrence as forecasts using probabilities, such as 40%, 70%, etc.
- Medical Diagnosis-Priests use probability models in deciding treatments.
- Finance & Investing-Risk analysis, stock predictions, portfolio optimization.
- Sports Analytics-By using probability, teams try to analyze winning odds.
- AI & Machine Learning-Uses of probability can be found in spam filters, recommendation systems, and speech recognition.
- Insurance Industry-Premium costs are based on risk probability.
- Quality Control in Manufacturing-Defect probabilities determine product reliability.
Is Probability Theory a Beginner’s Subject?
Not at all-understanding the fundamentals makes it a breeze. Start with coin tosses, dice rolls, and card problems. Add on gradually to formulas such as conditional probability or Bayes’ theorem.
The trick is associating problems with real-life conditions, not just the abstract mathematical symbols.
Advanced Concepts in Probability Theory
Once you’ve mastered the basics, you’ll find that this is where probability grows like a giant.
- Random Variables-The set of possible values associated with such a variable is the entire space of outcomes of a random phenomenon.
- Probability Distributions-Functions that specify their relative probabilities of occurrence (e.g., Normal Distribution, Binomial Distribution).
- Law of Large Numbers-As you repeat experiments, the results converge to expected probabilities.
- Central Limit Theorem-People assert that data distribution approaches normal in very large samples.
These are the concepts fueling machine learning, data science, and risk modeling.
Probability Theory in Data Science and AI
Data Science is probability theory with superpowers.
- Predictive Models-the fraud transaction detection is made possible through probabilities.
- Natural Language Processing-The word next in his text prediction is decided through probability.
- Recommendation Systems-Netflix makes a guess about a movie that becomes your next favorite because of probability.
Without probability, AIs would be just parrots repeating the past data, but with it, AIs become predictors.
The Language of Uncertainty Is Probability
Living is betting, whether betting large or small. Any time you step into a crosswalk, purchase a lottery ticket, or take a job, the probability stands there in the background.
Learning Probability Theory is like learning a private language – it is a secret code to read the uncertain and transform it into measurable, actionable insight.
Boost Your Career with PW Skills Data Science Course
Want to move from theory to actually using probability for real projects?
The course on Data Science offered by PW Skills bridges the gap between math and industry. Concepts like probability, statistics, machine learning, and predictive modeling are all learned under the tutelage of professionals. Whether one is a beginner or a professional, this course will help in developing practical skills suited for real-life jobs.
We use Probability Theory to measure and predict uncertainty about any event in the real world-whether a financial event, scientific scenario, or everyday life general decision. Yes, probability is at the base of almost all AI models in terms of their predictions, natural language processing, and recommendation systems. Probability models help doctors estimate how effective treatments are and how much risk patients may have for diseases. Basic formulas such as Classical Probability, Complementary Probability, Addition Rule, Multiplication Rule, Conditional Probability, and Bayes' Theorem form the nuclei of Probability Theory.FAQs
What is Probability Theory mainly meant for?
Is Probability Theory applicable in Artificial Intelligence?
Give an example of Probability Theory in health care.
What are the main formulas of Probability Theory?

