Fibonacci Series In Python | Fibonacci Number In Python

Q: How many methods are there to generate the Fibonacci sequence?

The Fibonacci series can be solved using loops, recursion or dynamic programming, and more.

Q: What is the time complexity of the Fibonacci series using dynamic programming?

The time complexity using dynamic programming memoization is O(n).

Q: Can I compute the Fibonacci Series in Python without using recursion?

Yes, we can use iteration to calculate the Fibonacci series using loops. We can also use famous formulas like Binet’s Formula.

Fibonacci Series in Python is a most sought-after intermediate-level programming question. It is often asked during many technical interviews. A Fibonacci number is a sequence of numbers in which every number in the sequence is added to the two previous numbers to find the current number. Let us read this article to write a program for printing the Fibonacci series in Python.

Table of Contents

What is the Fibonacci Series in Python?

Fibonacci Numbers in Python is a sequence of numbers in which each number is the sum of two preceding numbers. In mathematical terms, the Fibonannci Series in Python F(n) is defined as

F(0) = 0

F(1) = 1

F(n) = F(n-1) + F(n-2) for n>=2

So, the simplest Fibonacci series in Python is 0,1,1,2,3,5,8,13,21,34, and so on. Each subsequent number is calculated using the sum of the previous two numbers in the series. Let us know how to write the Fibonacci Series in Python.

Mathematical Interpretation of the Fibonacci Series in Python

Fibonacci Series F(n) is a simple recurrence relation that can be represented using F(n) = F(n-1) + F(n-2) where n is the number. There are two base cases in this problem F(0) =0 and F(1) =1. Fibonacci series is a number series where each number is the addition of the previous two numbers in the series. In mathematical terms, it can be called a ‘recurrence relation’. A recursion relation is an equation that uses recursion to define a sequence of numbers that can be calculated using preceding terms.

fibonacci series in python

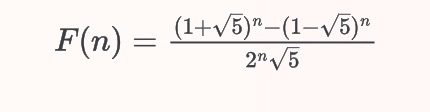
Using Binet’s Formula we can calculate the Fibonacci series in Python directly using mathematical expression using the golden ratio.

Fibonacci Series in Python (Binet’s Formula)

import math

def fibonacci(n):

phi = (1 + math.sqrt(5)) / 2

psi = (1 – math.sqrt(5)) / 2

return int((phi**n – psi**n) / math.sqrt(5))

Fibonacci Series in Python Using a Loop

Let us write a program to print the Fibonacci series in Python using a loop. We can use a ‘while’ loop or ‘for’ loop for the purpose.

Fibonacci Series in Python using Loop

def fibonacci_series(n):

a, b = 0, 1

for _ in range(n):

print(a, end=” “)

a, b = b, a + b

Fibonacci_series(10)

Output

Output

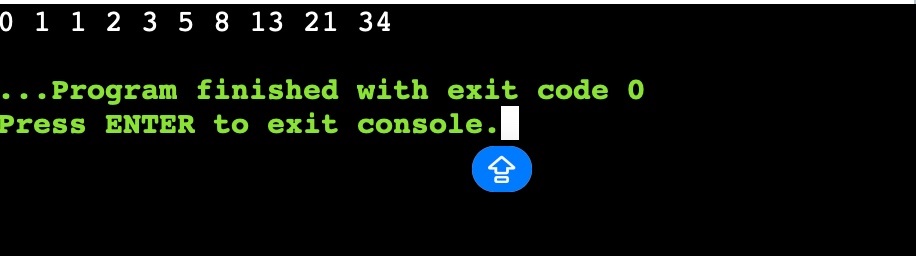
This function fibonnaci_series() takes two variables and assigns them with values 0 and 1. Now taking a for loop we keep on reassigning the value of a and b by assigning the value of b to a and assigning a+b to b. However, this function can only find the Fibonacci till a specified series.

Fibonacci Series in Python using Recursion

For recursion, we need a base case and repeated function call to print the Fibonacci series. Check the table below to print the Fibonacci Series using Python.

Fibonacci Series in Python using Recursion

def fibonacci_recursive(n):

if n <= 1:

return n

else:

return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

def print_fibonacci_series(n):

for i in range(n):

print(fibonacci_recursive(i), end=” “)

# Print Fibonacci series up to 10 numbers using recursion

print_fibonacci_series(10)

Output

Recursion

Here using the recursion function fibonacci_recursive() function we first take a base case when n is less than 1 and return the value of n. If n is greater than 1 then we call the sum of fibonacci_recursive(n-1) and fibonacci_recursive(n-2) repeatedly until the base case is reached.

Fibonacci Series in Python using Dynamic Programming

In Dynamic programming, we use the memoization approach to optimize the recursive method by storing the computed value in a variable to use later.

Fibonacci Series in Python using Dynamic Programming

memo = {0: 0, 1: 1}

def fibonacci_memoization(n):

if n in memo:

return memo[n]

memo[n] = fibonacci_memoization(n-1) + fibonacci_memoization(n-2)

return memo[n]

def print_fibonacci_series(n):

for i in range(n):

print(fibonacci_memoization(i), end=” “)

# Print Fibonacci series up to 10 numbers using memoization

print_fibonacci_series(5)

Output

Dynamic Programming

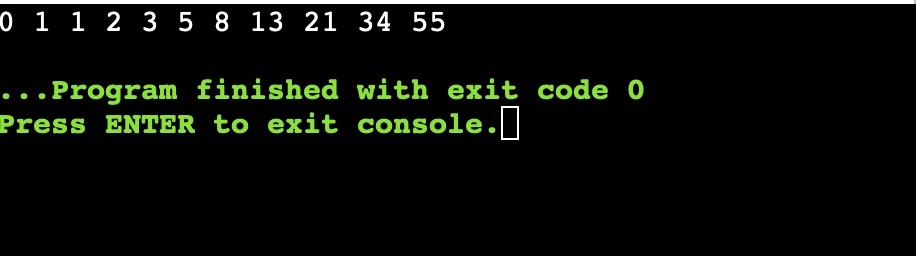
Here, using dynamic programming we store the value of 0 and 1 first in a variable memo. We created a function fibonacci_memoization() to find and print the Fibonacci series in Python using a dynamic programming approach. The time complexity of this approach is O(n) where n is the number.

Fibonacci Series in Python using Backtracking

We can use the backtracking approach of Python to print the Fibonacci series below.

Fibonacci Series in Python using Backtracking

def fibonacci(n, memo={}):

if n <= 0:

return 0

elif n == 1:

return 1

elif n in memo:

return memo[n]

else:

memo[n] = fibonacci(n-1) + fibonacci(n-2)

return memo[n]

print(fibonacci(7))

Here, we use the backtracking technique and recursion to print the Fibonacci series in Python. The function takes an argument n and an optional memo dictionary which is used to store Fibonacci values. If n is less than or equal to 0, the function returns 0 and 1.

If n is already present inside the memo then the function returns the stored value. If n is not in the memo then the function recursively calls the Fibonacci series using n-1 and n-2 terms and returns the value.

Learn Python Programming with PW Skills

If you are a beginner and want to learn Python Programming then enrol in our Decode Python with DSA Course to learn Python with interactive coursework and hands-on learning experience. Learn crucial concepts of Python with our experienced mentors. Get free interactive real-time industry projects, practice exercises, quizzes, doubt-free sessions, certification, and much more only at pwskills.com.