If we talk according to CLT, then no matter how many samples you take from a population, if the sample size is greater than or equal to 30 (n≥30), then the mean of the samples will be normally distributed. Also, the population distribution does not matter, whether it is normal or skewed.
If you are curious to understand and learn more about the Central Limit Theorem, then continue reading further as we will be discussing everything about C in this blog, including its formula, proof, applications, assumptions, and much more.
What Is The Central Limit Theorem In Statistics?
First of all, let us start by understanding the most basic yet most common question among students that What is the Central Limit Theorem? Well, the Central Limit Theorem or CLT is one of the most crucial pillars of statistics.
It states that if you take multiple samples from a population, then the mean of all those samples will be normally distributed and upon plotting them, you will get a bell-curve graph.
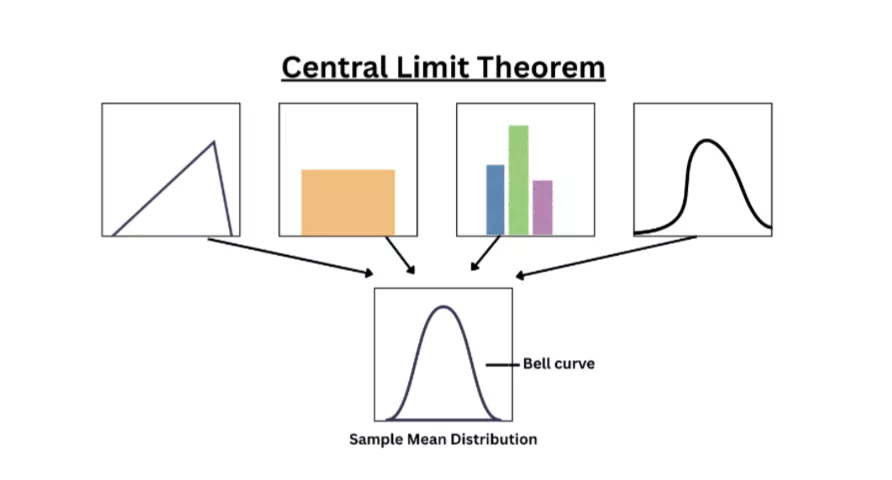
But there is one condition that you must keep in mind while taking samples. The sample size, which we represent by ‘n’, should always be greater than or equal to 30.
[n≥30]
When you do not know the population distribution, even then, the statisticians are able to draw conclusions. The Central Limit Theorem proves that the distribution of the sample mean will be the same as the population mean, and as the sample size increases, all types of mean distributions merge to a normal distribution.
Read More: A Complete Guide To Math And Statistics For Data Science
How Does The Central Limit Theorem Work?
The Central Limit Theorem is a method by which we can understand data in a better way. It basically states that if we take multiple random samples from a population and find their averages, then those averages will be in the form of a bell-shaped curve when plotted on the graph, which means a normal distribution.
CLT helps us to make the right decisions about the data by not actually working on huge data sets, but testing samples. It saves our time by avoiding the need to work and check each and every person’s data individually or check large datasets. The data collected is in huge numbers, and it is generally impossible for anyone to perform analysis on all of it.
Formula Of The Central Limit Theorem
To understand the formula of the central limit theorem, let us make some assumptions. Let:

- ‘X’ be any variable
- ‘𝜎’ be its standard deviation, and
- ‘μ’ be its mean
Now, the sample mean (x̅) will be a normal distribution, according to CLT.
The Z-score of X (random variable) will be Z = x̅ – μ/𝜎 / √n
For a clear understanding, you can check out the formula in the image below.
Importance Of The Central Limit Theorem
The Central Limit Theorem plays an important role as it is used almost everywhere. Have a look at some of the key reasons why CLT is considered important.
- It helps to draw conclusions even from samples.
- It saves time, as with the use of CLT, you do not have to work on large sets of the population, as it is impossible to work and analyse the whole data that has been collected.
- It allows accurate estimation of characteristics. When the number of samples is increased, the deviation of the sample mean from the population mean decreases. This eventually results in getting more apt outcomes.
Applications Of The Central Limit Theorem
The Central Limit Theorem is used at multiple places. From elections and textile production to food processing, the central limit theorem is applicable everywhere.
Check out some of the applications of the Central Limit Theorem (CLT) below.
- One of the places where Central Limit Theorem is used is the elections. With the Central Limit Theorem, you can estimate the number of people who support a specific candidate.
- CLT is also used to calculate various details, like family incomes, individual income, electricity consumption, and many more.
- CLT is even used in Textile Production. It is used by workers to measure the thickness of the fabric to ensure a fine quality product.
- Now, the next application might sound a bit strange, but yes, CLT is even used in food processing. It is especially used by factories that manufacture packaged products; they select some packages as samples and perform the checks.
Read More: What Is the Importance of Statistics for Data Science in 2024?
Assumptions Of The Central Limit Theorem
It is essential to know the assumptions we make for the Central Limit Theorem. The CLT is valid only if the following conditions are fulfilled. Let’s have a look at the assumptions of the Central Limit Theorem below.
- The sample you take from the population should be selected on a random basis.
- The samples must not be related to each other. They must all be independent and should not impact each other.
- One thing that you need to ensure while taking samples is that the sample size should not exceed ten percent (10%) of the total population when sampling is done without replacement.
Central Limit Theorem Example (Solved)
Apart from just learning the concepts, it is essential that we look into some of the practical problems. Check out the solved example below.
Example question: A random distribution has a mean of 12 and a standard deviation of 3. You are required to find the mean and standard deviation if a sample of 36 is drawn from the distribution.
Solution: Given- n = 36, μ = 12, σ = 3
Following the Central Limit Theorem, we get
μx̅ = μ = 12
Now, σx̅ = σ/√n = 3/√36
σx̅ = 0.5
Hopefully, the above example will make you understand how the questions related to CLT are solved. This was just one example; you can practice more, and you’ll understand the concept well with each question you move forward.
Central Limit Theorem FAQs
Q1. What does CLT stand for?
Ans: CLT stands for Central Limit Theorem.
Q2. What is the central limit theorem in statistics?
Ans: The Central Limit Theorem in statistics basically states that if you take multiple samples from a population, then the mean of all those samples will be normally distributed and upon plotting them, you will get a bell-curve graph.
Q3. What are the three main principles of CLT?
Ans: The whole concept of CLT is based on 3 mathematical concepts, they are:
1. Expectation
2. Variance
3. Covariance

