A Prime number is a number that is divisible by itself or by 1, such as 2, 3, 5, and so on. In this article, we will learn different ways to write a C program for checking whether a given number is prime or not.
When you’re starting out, it’s not just important to write code but also to understand how to explain a C program? Explaining helps build clarity and also prepares you for interviews and academic evaluations. In this guide, we’ll explore C programming examples with answers, structure, and the logic behind each program.
What are the functions in C?
Functions in C are the blocks of code which are designed to perform a specific task and an example is given below:
int add(int a, int b) {
return a + b;
}
What are the four basic types of C?
The four basic datatypes in c are:
- int – values that are in integer
- float – the values that are having decimals
- char – character
- double – values that are decimal with high precision.
What are the 4 Types of Functions in C?
- Function has no arguments and no return value.
- Function has arguments, but no return value.
- Function has arguments and return value.
- Function has no arguments but returns a value.
What are the 4 principles of c?
Though not officially defined, the guiding principles are as follows:
- Modularity
- Simplicity
- Efficiency
- Portability
What are the three methods of c programming?
You can categorize C programming methods as:
- Procedural – Using functions and structure.
- Modular – Divide big code in smaller functions.
- Structured – Readable and maintainable codes.
How to define in C program?
Constant definitions are made with the #define directive:
#define PI 3.14
How to write C program format?
Looking for Generic format of how to write C programs? Lets explore.
#include <stdio.h>
int main()
{
// Your code here
return0
}
Where Is C Mainly Used?
In operating systems (Linux kernel, for example)
- Embedded systems
- Firmware development
- Game
- Compilers
- System software
What are the three methods of C?
Although the C programming language does not have “methods” on a par with object-oriented languages such as Java or Python, these three core ways to structure and write logic in C are what students project among themselves. For example, they help beginners know the three ways to approach the basics of problem-solving in C.
-
Using Functions
This method is perhaps the most well-known in C programming. It pertains to dividing the code into reusable functions to make the program cleaner and modular.
Example: Writing a function with the task of computing the result of adding two numbers.
-
Using Pointers and Structures
C gives low-level memory access using pointers, and structures can group related variables together. One of the main approaches in dealing with dynamic memory, arrays, and file handling.
Example: Passing a structure by pointer to a function.
-
Using File Handling
Another main method that C adopts is file handling. Using fopen(), fprintf(), and fscanf() to read from and write to external files are some of the most common, real-world examples in C programming.
Example: Creating a file and having it hold student records.
Importance of These Methods
Understanding these methods will equip one with the necessary foundation for
- Writing scalable programs
- Handling some sort of real-world problem in C
- Understanding the basics of procedural programming
These three approaches huddle together in all the basic programs in C for beginners, who can thus get from simple logic blocks to full-fledged programs.
What is a Prime Number?
Any natural number that can be divided by both 1 and itself is called a prime number. There are only two factors in a prime number. For example, 2, 3, 5. 7, and so on. These prime numbers can be expressed as a product of two numbers such as 3 can be written as 1*3, 5 can be written as 5*1, etc. Explore What are 10 examples of C? Below in this article.
Write a Program to Check Whether a Number Is Prime or Not in C
Here’s a simple C program to check whether a number is prime or not:
#include <stdio.h>
int main() {
int num, i, isPrime = 1;
printf("Enter a number: ");
scanf("%d", &num);
if (num <= 1) {
isPrime = 0;
} else {
for (i = 2; i <= num / 2; i++) {
if (num % i == 0) {
isPrime = 0;
break;
}
}
}
if (isPrime)
printf("%d is a prime number.\n", num);
else
printf("%d is not a prime number.\n", num);
return 0;
}
🧪 Sample Output
Enter a number: 7
7 is a prime number.
This program checks divisibility from 2 to num / 2. If any divisor is found, it sets isPrime to 0.
This is a program to check whether a entered number is prime or not. Please help me where I am doing wrong?
byu/meresaathhikyu incpp_questions
Write a C Program to Check Whether the Given Number Is Prime or Not
Here’s a simple and efficient C program to check whether a given number is prime or not:
#include <stdio.h>
int main() {
int num, i, isPrime = 1;
printf("Enter a number: ");
scanf("%d", &num);
if (num <= 1) {
isPrime = 0;
} else {
for (i = 2; i * i <= num; i++) {
if (num % i == 0) {
isPrime = 0;
break;
}
}
}
if (isPrime)
printf("%d is a prime number.\n", num);
else
printf("%d is not a prime number.\n", num);
return 0;
}
✅ Sample Output:
Enter a number: 17
17 is a prime number.
📌 Explanation:
- A prime number has only two divisors: 1 and itself.
- The loop runs till
i * i <= numfor efficiency. isPrimeis used as a flag to determine if any divisor was found.
Write an Algorithm to Find a Number Is Prime or Not in C
Here’s a simple algorithm to check whether a number is prime or not in C:
✅ Algorithm to Check Prime Number in C
- Start
- Input an integer
num - If
num <= 1, it’s not prime → Print and stop - Loop from
i = 2tosqrt(num)- If
num % i == 0, it’s not prime → Print and stop
- If
- If no divisor found in the loop, then
numis prime - End
💡 C programs for Practice Example in Words:
Check if a number like 29 is divisible by any number between 2 and √29.
If none divide evenly, then 29 is prime.
Flowchart or C Code
Here you go! Below is the flowchart explanation and its corresponding C code for the “Check Whether a Number is Prime” algorithm.
✅ Flowchart Steps (Text-Based Format)
[Start]
↓
Input: num
↓
Is num ≤ 1?
↓ Yes ↓ No
Print "Not Prime" Initialize i = 2
↓
Is i * i ≤ num?
↓ No ↓ Yes
Print "Prime" Is num % i == 0?
↓ Yes ↓ No
Print "Not Prime" i++
↓ ↑
[End] ←←←←←←←←←←←←←←
🧠 C Code Based on This Flowchart
#include <stdio.h>
int main() {
int num, i, isPrime = 1;
printf("Enter a number: ");
scanf("%d", &num);
if (num <= 1) {
printf("%d is not a prime number.\n", num);
return 0;
}
for (i = 2; i * i <= num; i++) {
if (num % i == 0) {
isPrime = 0;
break;
}
}
if (isPrime)
printf("%d is a prime number.\n", num);
else
printf("%d is not a prime number.\n", num);
return 0;
}
🧾 Sample Output
Enter a number: 23
23 is a prime number.Write a C Program to Check Whether a Number Is Prime or Not
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself.
Examples: 2, 3, 5, 7, 11, 13, etc.
Numbers like 4, 6, 8, and 9 are not prime as they have additional divisors.
🧠 Logic to Check Prime Number
To determine if a number is prime:
- If number ≤ 1 → Not Prime
- Loop from
i = 2to√number - If number divisible by
i→ Not Prime - If no such divisor found → Prime
This avoids unnecessary checks beyond square root of the number, making the solution efficient.
🔁 Algorithm (Step-by-Step)
Step 1: Start
Step 2: Read the number (num)
Step 3: If num ≤ 1, print "Not Prime", stop
Step 4: Set flag = 1
Step 5: For i = 2 to sqrt(num)
If num % i == 0
flag = 0
break
Step 6: If flag == 1, print "Prime"
Else, print "Not Prime"
Step 7: End
📊 Flowchart (Text Version)
[Start]
↓
Input number → num
↓
Is num ≤ 1?
→ Yes → Print "Not Prime" → [End]
→ No → i = 2, flag = 1
↓
While i * i ≤ num
↓
If num % i == 0?
→ Yes → flag = 0 → break
→ No → i++
↓
Is flag == 1?
→ Yes → Print "Prime"
→ No → Print "Not Prime"
↓
[End]
🧪 C Program Code
#include <stdio.h>
int main() {
int num, i, isPrime = 1;
printf("Enter a number: ");
scanf("%d", &num);
if (num <= 1) {
printf("%d is not a prime number.\n", num);
return 0;
}
for (i = 2; i * i <= num; i++) {
if (num % i == 0) {
isPrime = 0;
break;
}
}
if (isPrime)
printf("%d is a prime number.\n", num);
else
printf("%d is not a prime number.\n", num);
return 0;
}
🧾 Sample Output
Enter a number: 7
7 is a prime number.
Enter a number: 20
20 is not a prime number.
💡 Key Points
- Prime check runs in O(√n) time.
- The check
i * i <= numis used instead ofi <= numfor better performance. - First filter is
num <= 1which handles invalid/edge input early.
C Program Algorithm to Check Prime Numbers using a Loop
Check the algorithm to write a C program for checking whether a prime number is a prime number.
- Step 1: Enter a number as Input which you want to check whether a number is prime or not.
- Step 2: Initialize a variable as a temp with 0.
- Step 3: Use a for loop to run a loop from 2 to n/2.
- Step 4: If the given number is divisible by the present iterator, then increment or continue temp.
- Step 5: If temp stays 0 then return “ Given number is a prime number.”
- Else,
- Then return “The given number is not a prime number.”
Implementation of C Program Using Loop for Checking Prime Number
Check the C program code in the table below to check whether the given number is prime or not. Let’s see C programming examples with output.
| C Program to check Prime number Using Loop |
| #include <stdio.h>
int main() { int i, num, temp = 0; // read input from user. printf(“Enter the number you want to Check for Prime: “); scanf(“%d”, &num); // Run loop for num/2 for (i = 2; i <= num / 2; i++) { // check if given number is divisible by any number. if (num % i == 0) { temp++; break; } } // check for the value of temp and num. if (temp == 0 && num != 1) { printf(“%d is a Prime number”, num); } else { printf(“%d is not a Prime number”, num); } return 0; } |
Output
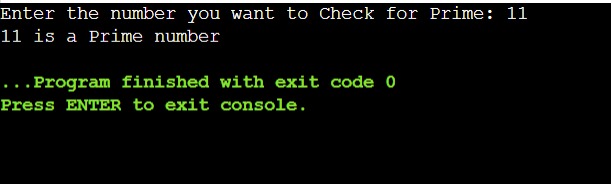
C Program Algorithm to Check Prime Number Using Functions
Check the algorithm for using the function to check whether a given number is prime or not.
- Step 1: Define a function which accepts an integer number as a parameter.
- Step 2: First, initialize a variable temp with 0.
- Step 3: Now iterate the loop from 2 to n/2.
- Step 4: If the given number is divisible by a loop iterator, then increment the temp value.
- Step 5: Now, check if the value of temp returned is 0. If it is 0 then return “Given number is Prime”
- Else,
- return “The given number is not a prime number.”
C Program Implementation to Check Prime Number Using Function
Check the code below in the table to check whether the given number is prime. Dive into c programming examples with output.
| C Program Code to Check Prime Number Using Function |
| #include <stdio.h>
// Function is used to check whether the number given is prime or Not int is_Prime(int num) { int i, temp = 0; // iterate up to num/2. for (i = 2; i <= num / 2; i++) { // if num has factors, // update temp. if (num % i == 0) { temp++; } } return temp; } int main() { int num, temp = 0; printf(“Enter the number you want to check for Prime: “); scanf(“%d”, &num); // Calling function temp = is_Prime(num); if (temp == 0 && num != 1) { printf(“\n %d is a Prime Number”, num); } else { printf(“\n %d is Not a Prime Number”, num); } return 0; } |
Output
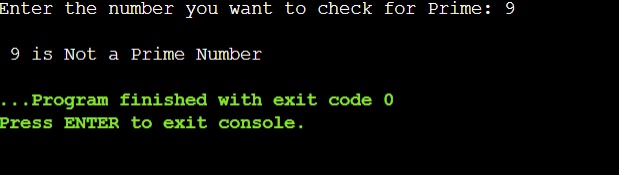
C Program Algorithm to Check for Prime Using Recursion
This is an algorithm to check whether a given number is prime or not using recursion.
- Step 1: Define a recursive function which accepts an integer as a parameter, say num.
- Step 2: Intialize the value of i with “2”/
- Step 3: Now, decide the base condition of the function. When the num value is equal to 0 or 1, the return is false.
- Step 4: If the num value is equal to i then return true.
- Step 5: If the num value is equal to i then return true.
- Step 6: If the number is divisible by i then return false and increment i.
- Step 7: Keep calling the function recursively until it reaches the base value.
C Program Implementation for Prime Number Using Recursion
Check the code below for the implementation of the prime number checker function using the recursion function.
| C Program to Check for Prime Number Using Recursion |
| #include <stdio.h>
#include <stdbool.h> // Recursive function to check for prime number bool is_Prime(int num) { static int i = 2; // Base Case if (num == 0 || num == 1) { return false; } // Recursive Case if (num == i) return true; // check if num is divisible by any number if (num % i == 0) { return false; } i++; // recursive function call. return is_Prime(num); } int main() { // test case 1 int num = 20; if (is_Prime(num)) { printf(“%d is a Prime number\n”, num); } else { printf(“%d is not a Prime number \n”, num); } } return 0; } |
Output
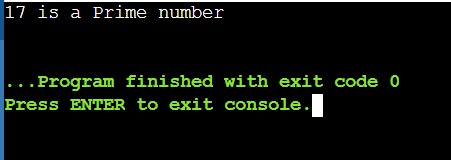
C Program Algorithm to Check for Prime Number using Sieve of Eratosthenes
The Sieve of Eratosthenes is an efficient way of finding all prime numbers smaller than a given number n when n is smaller than 10 million or so. Given below is the algorithm to check for Prime numbers using the Sieve of Eratosthenes.
- Step 1: Make an array of type boolean is_Prime[] and itntialize all its indexes with a value of 1 or true.
- Step 2: Start with the first number, which will be 2.
- Step 3: Iterate over each number from 2 to the square root of n.
- Step 4: For each prime number, mark its multiples as non-prime in the array of is_Prime.
- Step 5: The numbers in the array that are still true are prime numbers. Now return i.
C Program Implementation to Check for Prime Number using Sieve of Eratosthenes
Check the code below for implementation of Sieve of Eratosthenes in the table below.
| C Program to Check for Prime Number using Sieve of Eratosthenes |
| #include <stdio.h>
#include <stdbool.h> void sieve_of_eratosthenes(int n) { // Create a boolean array with all values marked as true bool is_prime[n+1]; for (int i = 0; i <= n; i++) { is_prime[i] = true; } // Start with the first prime number, which is 2. for (int p = 2; p * p <= n; p++) { // If is_prime[p] is not changed, then it is a prime if (is_prime[p] == true) { // Update all multiples of p to not prime for (int i = p * p; i <= n; i += p) { is_prime[i] = false; } } } // Print all prime numbers printf(“Prime numbers up to %d are: “, n); for (int p = 2; p <= n; p++) { if (is_prime[p]) { printf(“%d “, p); } } printf(“\n”); } int main() { int n; printf(“Enter a number to find all prime numbers up to: “); scanf(“%d”, &n); sieve_of_eratosthenes(n); return 0; } |
Output
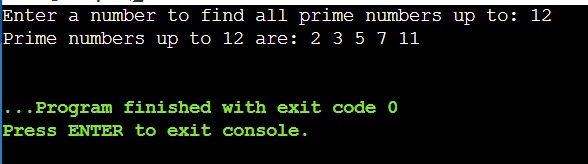
Learn C Programming Online: Resources
You can learn C programming online via:
- TutorialsPoint
- GeeksforGeeks
- CodeChef
- HackerRank
- Coursera & edX
- PW Skills
Learn Data Structure in C++ with PW Skills
If you want to sharpen your Data Structures and Algorithms for a Software developer role, then start your transformation journey with our Decode C++ with DSA Course and master C++ programming along with major DSA Concepts.
Get more than 100+ hours of learning materials, all covered by industry-level experts. Have access to the latest curriculum based on cutting-edge technologies with free PW Lab access, Q&A dashboard, industry-relevant project-based learning, certification and much more only at pwskills.com.
C Program for Prime Numbers FAQs
How do I find prime numbers from 1 to 100 using the C program?
We can use the Sieve of Eratosthenes to print prime numbers in a given range from a given prime number to a given value n.
How do you check whether a given number is prime or not?
If a number is divisible by itself or by 1, then it is said to be a prime number. We can use c program to find if a number is prime or not.
What are different ways of checking whether a number is prime or not?
We can use loops, functions, recursions and other methods to check whether a given number is prime or not.
What is the sieve of Eratosthenes in C?
The sieve of Eratosthenes is an algorithm to find all prime numbers in a segment from the given prime number to n. Check out more about the algorithm in this article.

